Investigación
Modelaje matemático con la ecuación de Gompertz y sus aplicaciones en crecimiento de pollos de engorde
Para leer más contenidos de aviNews España Octubre 2023
Investigación
Para leer más contenidos de aviNews España Octubre 2023
La producción de pollos de engorde se ha vuelto cada día más especializada y esta industria demanda una gran cantidad de análisis de datos de manera constante.
La necesidad de estar realizando análisis más profundos ayudan a las compañías productoras de carne de pollos a poder tomar mejores decisiones.
Y, por ende, mayor retorno de la inversión en sus flujos efectivos y en sus ganancias.
La ecuación matemática de Gompertz es una ecuación que se puede utilizar como una herramienta en el análisis de datos para la producción de pollos de engorde.
Los datos que arroja esta ecuación son muy diferentes a los que estamos acostumbrados a observar en las fichas de producción de las diferentes estirpes de pollo.
El objetivo principal de este artículo consiste en describir de manera práctica y sencilla la ecuación de Gompertz y sus aplicaciones zootécnicas y administrativas en una producción de pollo de engorde.
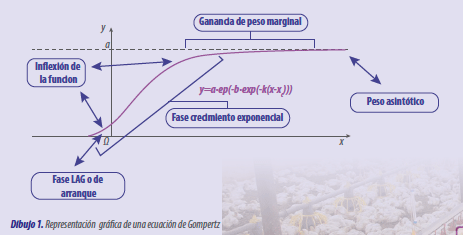
La ecuación de Gompertz la siguiente manera: describe de manera matemática eventos no lineales, o dicho en otras palabras, el crecimiento de pollo puede ser descrito por la función de la ecuación.
Cuando hablamos de ajuste, estamos haciendo referencia a la línea que mejor describe los datos en un eje X/Y.
La información que necesitamos para obtener los coeficientes de esta ecuación es la variable tiempo, la cual puede ser en días o semanas.
Por otro lado, la otra variable que necesita esta ecuación es la variable peso en cada una de los días o semanas que los pollos fueron pesados.
La ecuación de Gompertz se escribe de la siguiente manera:
Y= a * EXP (-EXP(-b(X-c))
Los parámetros que se describen en esta ecuación son:
Mencionar que esta ecuación te ayuda a obtener un peso, pareciera que no hace mucho sentido.
Pero cuando nos sumergimos en el análisis de datos, vamos a observar todos los parámetros que esta ecuación nos puede proporcionar.
En el Dibujo 1 se describen cada uno de los coeficientes que componen la ecuación de Gompertz.
Ya hemos descrito que la ecuación nos permite modelar el peso de un lote.
Con la derivada de esta ecuación, podemos obtener la proyección de ganancia de peso diaria de un lote de producción.
Esta derivada de la ecuación se describe como:
Ganancia de Peso = a*Peso Modelado *EXP(c*(b-Tiempo))
Las variables incluidas en la derivada de la ecuación se describen como:
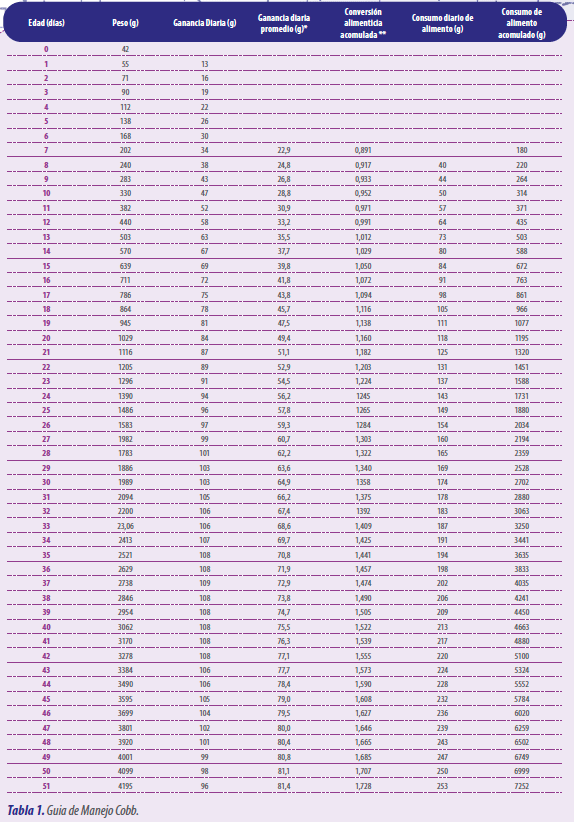
La información de donde se obtienen los coeficientes es a partir de datos de la guía de manejo.
A manera de ejercicio, los datos utilizados fueron obtenidos a partir de las guías de manejo de las estirpes Ross y Cobb.
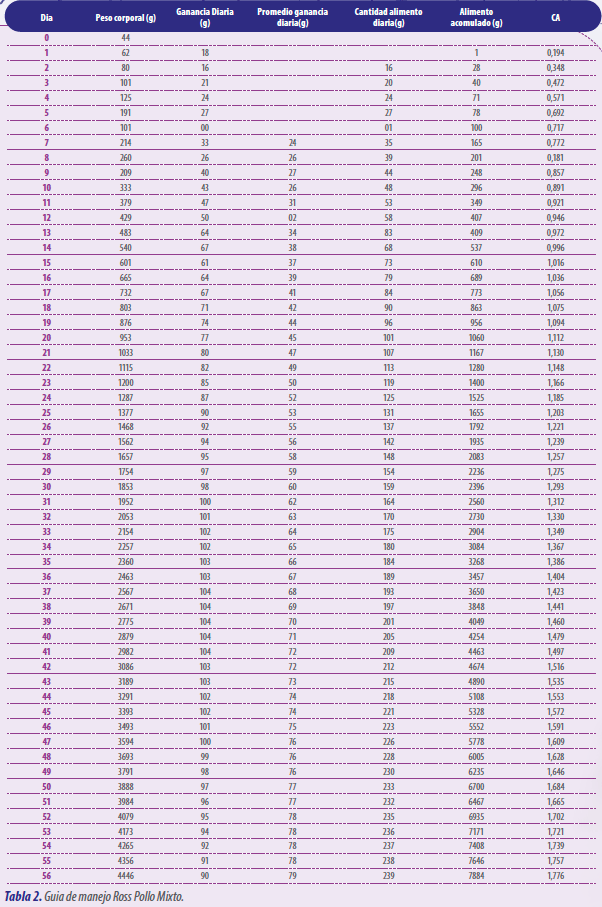
Estos coeficientes se obtienen con la ayuda de softwares en matemática, en donde se debe de escribir la programación respectiva para que arranque una ecuación no lineal.
Luego de obtener los coeficientes, comenzamos a generar información que puede ayudar a una mejor toma de decisiones financieras y zootécnicas.
En la siguiente tabla se presentan las otras variables que podemos obtener utilizando los coeficientes de la ecuación de Gompertz.
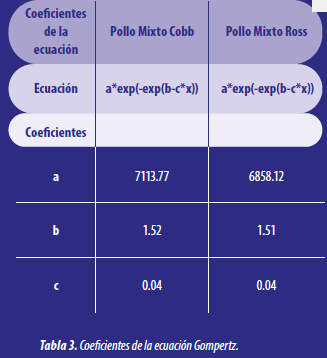
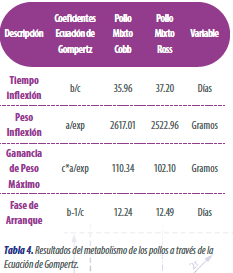
En la tabla que se presenta a continuación, se presentan los coeficientes que componen la ecuación de Gompertz.
Cuando se combinan los coeficientes de la ecuación se pueden obtener descripciones específicas de la curva.
Por ejemplo, cuando se dividen los coeficientes b/c, esta variable describe el punto de la gráfica en donde se da una de las inflexiones, pero en función del tiempo.
Esta variable nos indica que a partir de los días 35.96 y 37.20 los pollos de estas estirpes crecen exponencialmente hasta ese periodo de tiempo.
Si se divide a/EXP, esta variable describe el peso del pollo al momento de la inflexión.
El significado de esto se refiere a que cuando se alcanza el día 35.96 y 37.20 los pollos tienen un peso proyectado de 2617.01 y 2522.96 gramos respectivamente.
La variable Ganancia de Peso máxima, la cual se escribe como c*a/EXP, hace referencia a la máxima ganancia de peso que los pollos alcanzan en su vida productiva.
De acuerdo a los datos del modelaje, un pollo COBB la máxima ganancia que puede desarrollar es de 110 gramos de ganancia en un día y el pollo ROSS mixto nos estaría aportando una ganancia máxima de peso de 102.10 gramos en un día.
Algo que se debe de comentar es que esta sensibilización tomó los datos del día 1 hasta el día 56.
Esto es un dato importante a comentar cuando de modelaje se trata, ya que los coeficientes y las tasas cambian cuando la variable tiempo se utiliza con diferentes amplitudes.
Esto quiere decir que no es la misma ecuación cuando se hace un modelaje de día 1 a día 42 y otra ecuación que describa el período de tiempo del día 1 al día 56.
La última variable, fase de Arranque o fase LAG, se describe como b-1/c.
Esta última hace referencia a la cantidad de días en que el metabolismo del pollo está completamente maduro para que la formación de carne se genere de manera exponencial.
Cuando se analiza la ecuación de Gompertz, se observa que trabaja a partir de tasas o índices y estas variables describen de forma numérica el metabolismo de un animal.
Esto permite trasladar ese metabolismo a un número que describe perfectamente el estadío por el cual está desarrollándose el animal.
¿CÓMO OBTENER LOS COEFICIENTES DE LA ECUACIÓN DE GOMPERTZ?
Los coeficientes de la ecuación de Gompertz, se obtienen a partir de los datos de crecimiento que se desean modelar.
Ahora bien, el cálculo de los coeficientes de la ecuación se obtienen a partir de programas matemáticos.
Algo a mencionar, es que esta es una matemática no lineal, por lo tanto la descripción de esta no necesita de cálculos más avanzados.
No debemos frustrarnos cuando se habla de matemática no lineal, ahora existen programas que nos pueden ayudar a gestionar los datos de crecimiento.
Algunos de los programas que nos pueden ayudar a utilizar esta información pueden ser: R, Rsutdio o SAS.
Pueden haber otros programas, pero estos son los de uso más frecuente.
En el caso de R o Rstudio, son software gratis y en ellos se puede descargar los paquetes de cálculo de matemática no lineal.
A continuación, se mencionan algunos paquetes que puede ayudar a calcular esta ecuación:
La ecuación de Gompertz nos puede ayudar dentro de una compañía de pollo de engorde a:
Implementar programas de nutrición de precisión en pollo de engorde para realizar el cambio de alimento en el momento de tiempo y peso exacto.
No debemos de olvidar que el crecimiento de un pollo es la descripción del metabolismo, por lo tanto esta ecuación permite observar en qué momento el metabolismo de un pollo cambia.
Con el cálculo de la derivada de la ecuación, se puede determinar si los cambios de una ración están permitiendo alcanzar la ganancia de peso proyectada por día o por semana.
Con ella podemos proyectar y realizar presupuestos administrativos más exactos. Utilizar ecuaciones matemáticas n o lineales permite predecir el desempeño de aquellos lotes que aún no se han sacrificado.
La proyección de escenarios hipotéticos utilizando Gompertz, le permite a una empresa reaccionar más rápidamente frente a desafíos de precios bajos en el kilo de pollo o una sobre oferta de pollo vivo en el mercado.
Si hubiera algún cambio del perfil nutricional, el nutrólogo podría percatarse inmediatamente si el pollo está respondiendo a estaración. La ecuación ayuda a modelar el metabolismo de crecimiento o tasas de cambio.
Por lo tanto, cualquier cambio en ellos permitiría observar si el desempeño está generando ganancias o pérdidas en el crecimiento de un pollo de engorde.
La ecuación de Gompertz, ayudaría a implementar programas de alimentación más exactos y con mayor retorno de inversión a una compañía.
En resumen, la ecuación de Gompertz ayuda a predecir y obtener tasas de crecimiento en función de peso y tiempo.
De esta forma, el uso continuo del modelaje matemático no lineal le permite a una compañía implementar programas alimenticios más eficientes y con mayor retorno en sus finanzas.
