Modelagem matemática com a equação de Gompertz e suas aplicações no crescimento de frangos de corte
A produção de frangos de corte tem se especializado cada dia mais e esse setor exige uma grande quantidade de análise de dados de forma constante. A necessidade de realizar análises mais aprofundadas auxilia as empresas produtoras de carne de frango a tomarem melhores decisões. E, portanto, maior retorno do investimento nos seus fluxos de caixa e lucros.
A equação matemática de Gompertz é uma equação que pode ser utilizado como ferramenta na análise de dados para produção de frangos de corte. Os dados fornecidos por esta equação são muito diferentes daqueles que estamos habituados a ver nas fichas de produção das diferentes linhagens de frango.
O objetivo principal deste artigo é descrever de forma prática e simples a equação de Gompertz e suas aplicações zootécnicas e administrativas na produção de frangos de corte.
A equação de Gompertz descreve matematicamente eventos não lineares, ou em outras palavras, o crescimento das galinhas pode ser descrito pela função da equação.
Existem muitas equações matemáticas não lineares, mas a equação de Gompertz demonstrou ter o melhor ajuste, gerada com dados de crescimento agrícola. Quando falamos em ajuste, estamos nos referindo à linha que melhor descreve os dados no eixo X/Y. A informação que necessitamos para obter os coeficientes desta equação é a variável tempo, que pode estar em dias ou semanas.
Por outro lado, a outra variável que esta equação necessita é a variável peso em cada um dos dias ou semanas em que os frangos foram pesados.
A equação de Gompertz é escrita da seguinte maneira:
Y= a * EXP (-EXP(-b(X-c))
Os parâmetros descritos nesta equação são:
Y = peso do animal em um período determinado (dias ou semanas)
X = dias (referente ao dia de crescimento em que o peso foi coletado)
a = peso assintótico (variável que descreve a linha reta que se aproxima indefinidamente de uma curva, sem nunca tocá-la)
b = taxa ou índice de maturação para a variável peso
c = ponto de inflexão para a variável idade
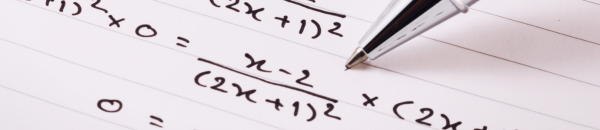
Mencionar que essa equação ajuda a obter um peso pode parecer que não faz muito sentido. Mas, quando mergulhamos na análise de dados, vamos observar todos os parâmetros que essa equação pode nos fornecer.
No Desenho 1, são descritos cada um dos coeficientes que compõem a equação de Gompertz.
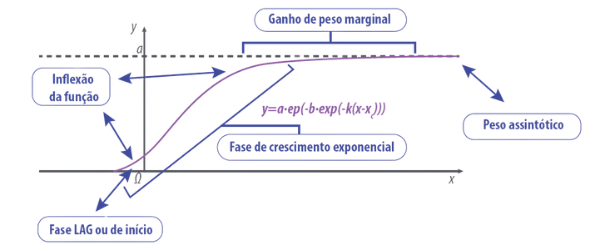
Desenho 1. Representação gráfica de uma equação de Gompertz.
Já mencionamos que a equação nos permite modelar o p...
